Supply, demand, surplus, DWL, and elasticity

If you have a formula for a supply curve and a demand curve, you can calculate all sorts of things, including the market clearing price, or where the two lines intersect, and the consumer and producer surplus. If taxes are involved, you can also calculate new market prices and quantities, deadweight loss (or the loss of market efficiency that comes from the tax), the total tax revenues raised, and the tax burden on consumers and producers.

Because this is a foundational concept in microeconomics, there are a billion YouTube videos with examples. Here are some of the best:

Khan Academy has a whole unit on consumer and producer surplus + market interventions here, including these:
Jodi Beggs has a ton of videos related to supply and demand (start here)
Jacob Clifford has an entire unit on supply and demand here

Supply, demand, surplus, DWL, and burdens

Here’s how to analyze a market with these equations:

$$ \begin{aligned} \text{S} &: P = 2 + 0.25Q \\ \text{D} &: P = 20 - 0.5Q \\ \text{S}_\text{tax} &: P = 2 + 0.25Q + 5 \end{aligned} $$

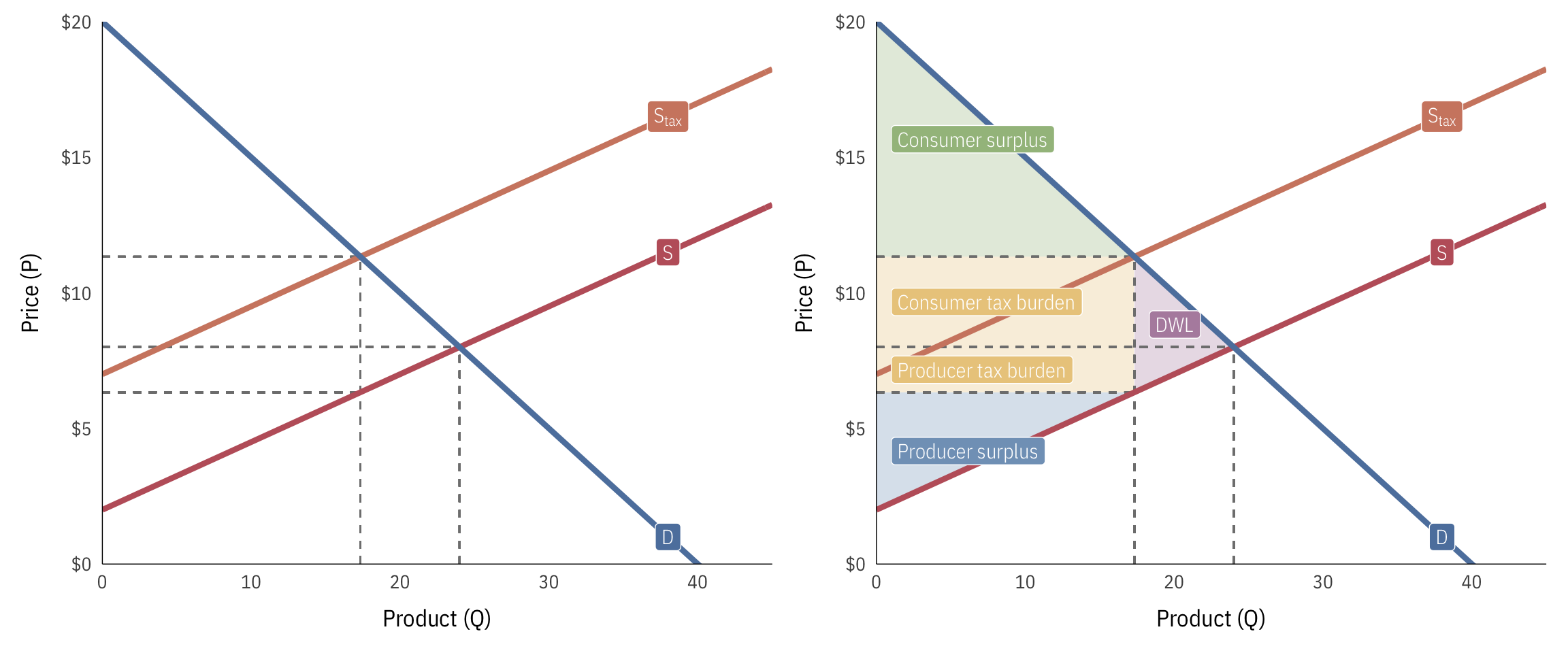
Pre-tax quantity: 24
Pre-tax price: $8
Pre-tax consumer surplus: $144 ($1/2 \times 24 \times 12$)
Pre-tax producer surplus: $72 ($1/2 \times 24 \times 6$)

Post-tax quantity: 17.33
Post-tax price: $11.33
Post-tax consumer surplus: $75.11 ($1/2 \times 17.33 \times 8.67$)
Post-tax producer surplus: $37.56 ($1/2 \times 17.33 \times 4.33$)

Deadweight loss: $16.67 ($1/2 \times 6.67 \times 5$)

Total tax incidence (revenue raised): $86.67 ($(11.33 - 6.33) \times 17.33$)
Consumer tax incidence: $57.78 ($(11.33 - 8) \times 17.33$)
Producer tax incidence: $28.89 ($(8 - 6.33) \times 17.33$)
Percent of tax borne by consumers: 67% ($57.78 / 86.67$)
Percent of tax borne by producers: 33% ($28.89 / 86.67$)

Elasticity and tax burdens

The burden of taxes (and the size of deadweight loss) depends on how elastic supply and demand are. Those who are most able to escape taxes (i.e. those who are most elastic) will avoid them, leaving the burden of taxes to the other more inelastic party. Here are a few different examples of taxes imposed on producers and consumers with varying elasticities:

Elastic demand

Here, demand is highly elastic—as the price changes, people change their consumption of the good quickly (i.e. increasing the price makes people jump away from it). Because of this, the burden of the tax falls on the producers, who can’t escape the tax. The tax also causes a lot of DWL because of the high elasticity.

$$ \begin{aligned} \text{S} &: P = 2 + 0.25Q \\ \text{D} &: P = 10 - 0.05Q \\ \text{S}_\text{tax} &: P = 2 + 0.25Q + 5 \end{aligned} $$

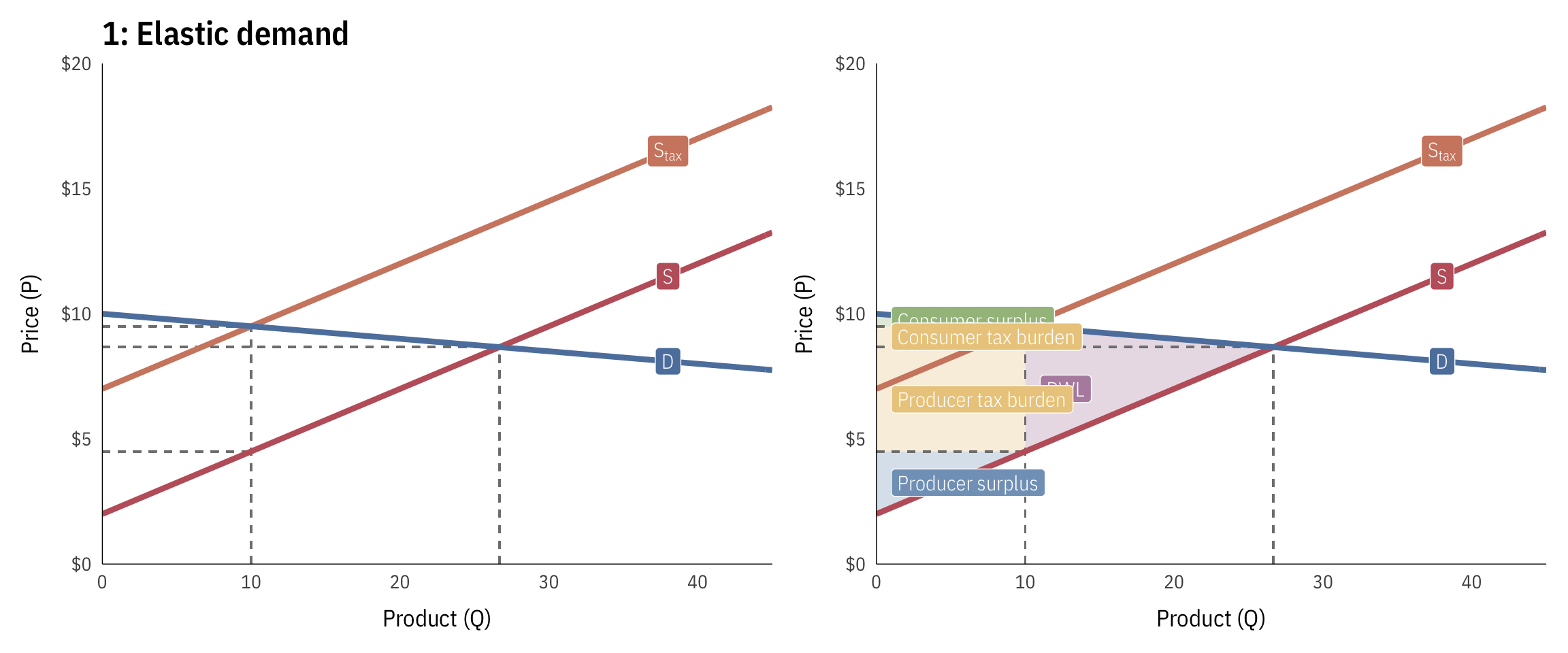
Pre-tax quantity: 26.67
Pre-tax price: $8.67
Pre-tax consumer surplus: $17.78 ($1/2 \times 26.67 \times 1.33$)
Pre-tax producer surplus: $88.89 ($1/2 \times 26.67 \times 6.67$)

Post-tax quantity: 10
Post-tax price: $9.5
Post-tax consumer surplus: $2.5 ($1/2 \times 10 \times 0.5$)
Post-tax producer surplus: $12.5 ($1/2 \times 10 \times 2.5$)

Deadweight loss: $41.67 ($1/2 \times 16.67 \times 5$)

Total tax incidence (revenue raised): $50 ($(9.5 - 4.5) \times 10$)
Consumer tax incidence: $8.33 ($(9.5 - 8.67) \times 10$)
Producer tax incidence: $41.67 ($(8.67 - 4.5) \times 10$)
Percent of tax borne by consumers: 17% ($8.33 / 50$)
Percent of tax borne by producers: 83% ($41.67 / 50$)

Inelastic demand

Here, demand is highly inelastic—as the price changes, the quantity doesn’t change a lot (i.e. increasing the price makes only a few people jump away, and the people who keep buying it have to suck up the higher price). Because of this, the burden of the tax falls on the consumers, who can’t escape the tax. The tax also causes smaller DWL because of the low elasticity.

$$ \begin{aligned} \text{S} &: P = 2 + 0.25Q \\ \text{D} &: P = 20 - 2Q \\ \text{S}_\text{tax} &: P = 2 + 0.25Q + 5 \end{aligned} $$

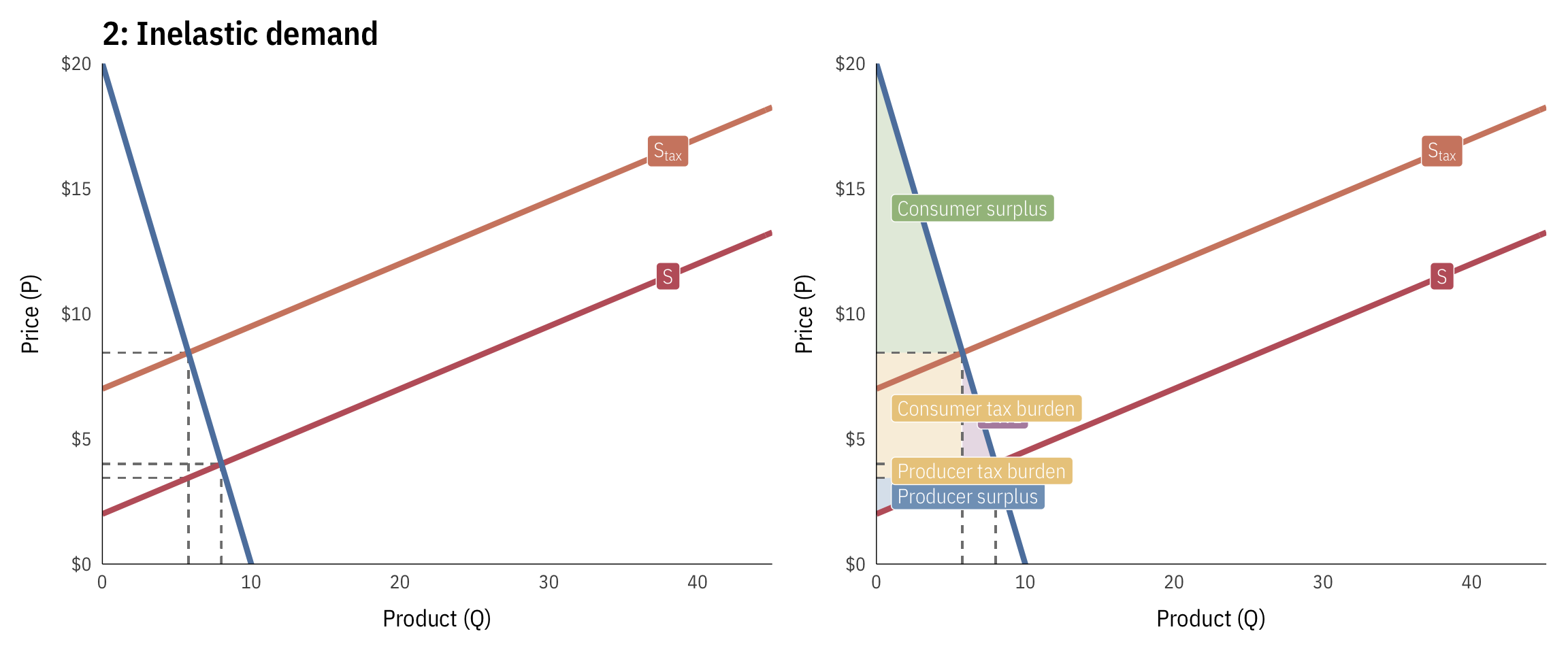
Pre-tax quantity: 8
Pre-tax price: $4
Pre-tax consumer surplus: $64 ($1/2 \times 8 \times 16$)
Pre-tax producer surplus: $8 ($1/2 \times 8 \times 2$)

Post-tax quantity: 5.78
Post-tax price: $8.44
Post-tax consumer surplus: $33.38 ($1/2 \times 5.78 \times 11.56$)
Post-tax producer surplus: $4.17 ($1/2 \times 5.78 \times 1.44$)

Deadweight loss: $5.56 ($1/2 \times 2.22 \times 5$)

Total tax incidence (revenue raised): $28.89 ($(8.44 - 3.44) \times 5.78$)
Consumer tax incidence: $25.68 ($(8.44 - 4) \times 5.78$)
Producer tax incidence: $3.21 ($(4 - 3.44) \times 5.78$)
Percent of tax borne by consumers: 89% ($25.68 / 28.89$)
Percent of tax borne by producers: 11% ($3.21 / 28.89$)

Elastic supply

Here, supply is highly elastic—as the price changes, the quantity produced changes a lot (i.e. increasing a tax on books would make Amazon redirect its efforts to music, video, or web servers and wouldn’t hurt the company that much). Because of this, the burden of the tax falls on the consumers, since the company escapes the tax easily. The tax also causes a lot of DWL because of the high elasticity.

$$ \begin{aligned} \text{S} &: P = 2 + 0.05Q \\ \text{D} &: P = 20 - 0.5Q \\ \text{S}_\text{tax} &: P = 2 + 0.05Q + 5 \end{aligned} $$

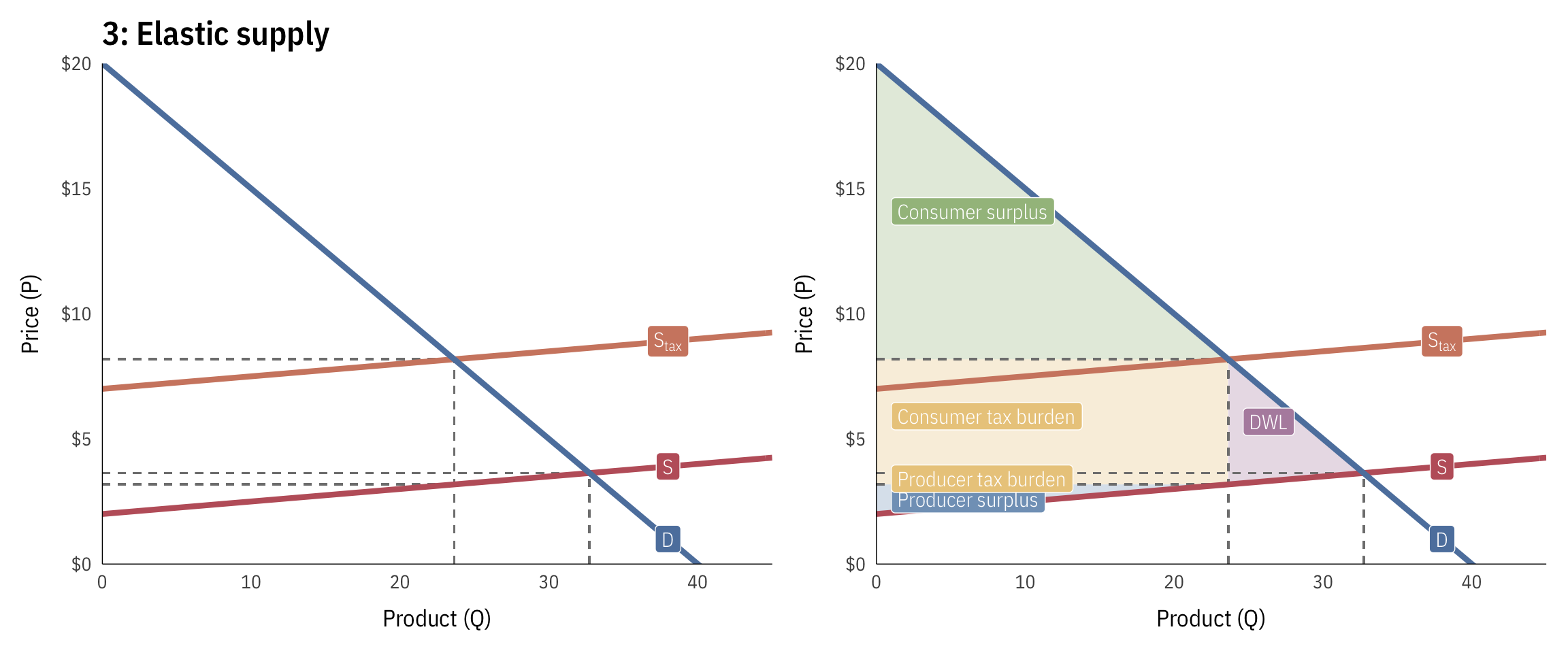
Pre-tax quantity: 32.73
Pre-tax price: $3.64
Pre-tax consumer surplus: $267.77 ($1/2 \times 32.73 \times 16.36$)
Pre-tax producer surplus: $26.78 ($1/2 \times 32.73 \times 1.64$)

Post-tax quantity: 23.64
Post-tax price: $8.18
Post-tax consumer surplus: $139.67 ($1/2 \times 23.64 \times 11.82$)
Post-tax producer surplus: $13.97 ($1/2 \times 23.64 \times 1.18$)

Deadweight loss: $22.73 ($1/2 \times 9.09 \times 5$)

Total tax incidence (revenue raised): $118.18 ($(8.18 - 3.18) \times 23.64$)
Consumer tax incidence: $107.44 ($(8.18 - 3.64) \times 23.64$)
Producer tax incidence: $10.74 ($(3.64 - 3.18) \times 23.64$)
Percent of tax borne by consumers: 91% ($107.44 / 118.18$)
Percent of tax borne by producers: 9% ($10.74 / 118.18$)

Inelastic supply

Here, supply is highly inelastic—as the price changes, the quantity produced changes a little (i.e. increasing a tax on books would put strain on a small family-owned bookstore that only sold books, since they’d have no other alternative things to produce). Because of this, the burden of the tax falls on the producers, since the company can’t escape the tax by doing other things.

$$ \begin{aligned} \text{S} &: P = 2 + 1.5Q \\ \text{D} &: P = 20 - 0.5Q \\ \text{S}_\text{tax} &: P = 2 + 1.5Q + 5 \end{aligned} $$

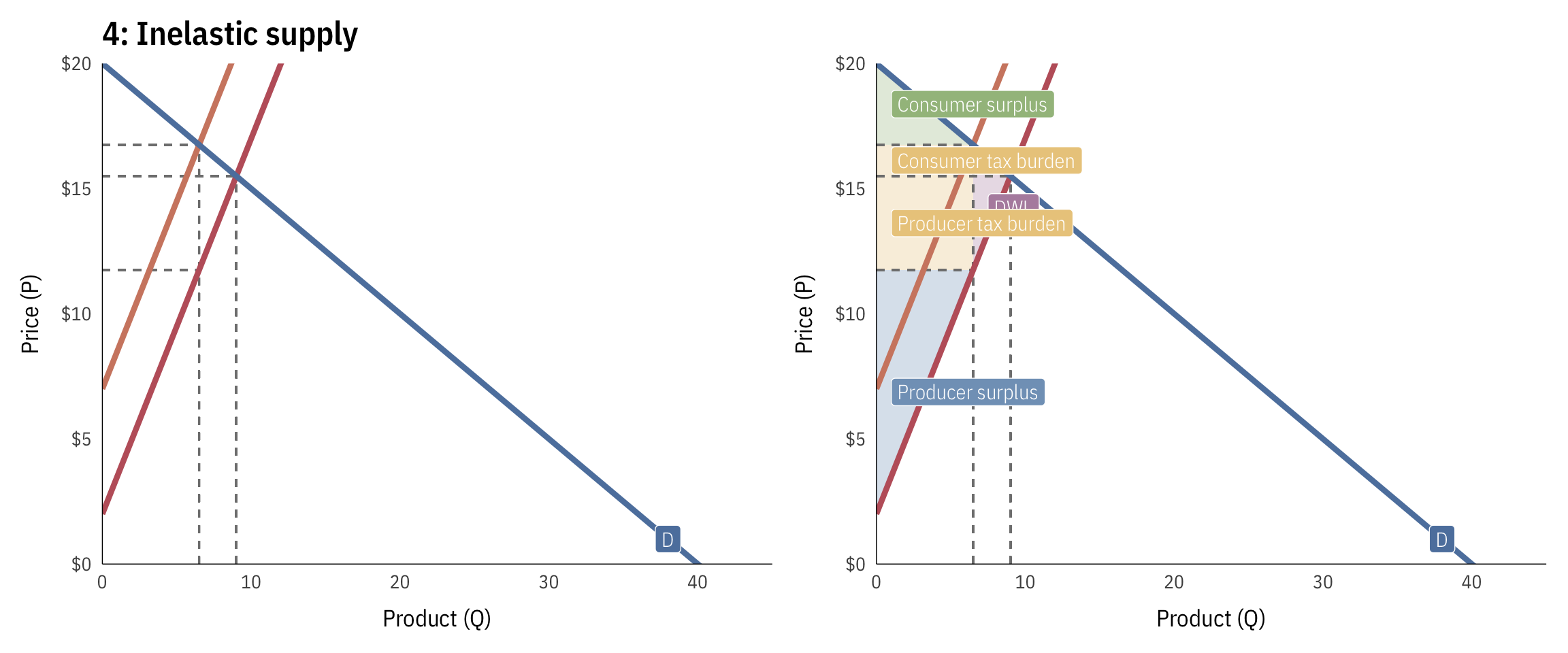
Pre-tax quantity: 9
Pre-tax price: $15.5
Pre-tax consumer surplus: $20.25 ($1/2 \times 9 \times 4.5$)
Pre-tax producer surplus: $60.75 ($1/2 \times 9 \times 13.5$)

Post-tax quantity: 6.5
Post-tax price: $16.75
Post-tax consumer surplus: $10.56 ($1/2 \times 6.5 \times 3.25$)
Post-tax producer surplus: $31.69 ($1/2 \times 6.5 \times 9.75$)

Deadweight loss: $6.25 ($1/2 \times 2.5 \times 5$)

Total tax incidence (revenue raised): $32.5 ($(16.75 - 11.75) \times 6.5$)
Consumer tax incidence: $8.12 ($(16.75 - 15.5) \times 6.5$)
Producer tax incidence: $24.38 ($(15.5 - 11.75) \times 6.5$)
Percent of tax borne by consumers: 25% ($8.12 / 32.5$)
Percent of tax borne by producers: 75% ($24.38 / 32.5$)

Last updated on January 1, 0001

Edit this page